代写之家创办11年以来,接过无数的留学生考试,作业的代写代考代做单子,经验之丰富不是一般野鸡机构能比拟的。每次接单之前,我们都会对学生给出的资料进行详细的评估,而后做出是否能胜任的决定,绝不是一般同行碰到单子就满口承若接下,压根不去做接单前的资料评估而随意接单,导致后续考试时候做不出任何题目,也请大家擦亮眼睛,多花点耐心去甄别所托之人是否负责靠得住。代写之家将继续秉承“一次合作,终生朋友”的信念服务好大家,继续为家人们的学业保驾护航!
以下是我们实际接过的部分科目代码详情,由于篇幅有限,不能把所有科目课程列举完毕,仅供大家参考,看下有无自己实际需要的科目。学生范围覆盖了美国,加拿大,英国,澳大利亚,新加坡,德国,俄罗斯,意大利,瑞士等国际,以及香港,澳门,台湾地区。科目范围涵盖了数学,物理,化学,经济学,金融学,计算机,电气工程等本硕方向的专业。
数学类:Pre-Calculus Math 12,MATH 1014 Calculus II,MATH2011 Intro to Multivariable Calculus ,Math 221 Calculus I,MA 1201,Math 231.Calculus ll,Math 241 Calculus III,MAT236,MATA37 Calculus,MAT232 Calculus of Several Variables,Math 1B – Calculus,MATH2323 GENERAL MATHEMATICS 1,MAST10006 Calculus 2 MAST10006 Calculus 2,MATH 53 Multivariable Calculus,Math 151 — Calculus II,Math 20E,MATH 152,MATH 156 – Calculus for Business and Economics II,Math 3140/2310,Math 10C,Math 263,Math 1322 ,Math1206,Math 2300 Calculus III,MA 411,Math 125,ENG2005 Advanced Engineering Mathematics,MA2006 Real Analysis,MAT 2125 Elementary Real Analysis,Math 597 REAL ANALYSIS,Math 3050/6050,Math UA 325 Real ,MATHEMATICS 2A VECTOR CALCULUS & COMPLEX ANALYSIS,Analysis,STAT 20 Introduction to Probability and Statistics,PROBABILITY AND STATISTICS, ECON 15A,Stat 134,Stat 151,ACTL 2131 Probability and Mathematical StatisticsACTL 5101 Probability and Statistics for Actuaries,37252 Regression and Linear Models,MATH STAT 302 Introduction to Probability,MATH 6420 – Mathematical Statistics II,STAT 311 Probability Theory,STAT GR5204 Statistical Inference,STAT3021 Stochastic Processes,STAT3600 LINEAR STATISTICAL ANALYSIS,MATH 6105 Mathematics for Science 1,MATHOO42-MATHEMATICAL METHODS lNCHEMISTRY,ADVANCED MATHEMATICS MCD4490,MATH 2033 Mathematical Analysis,AMA 2111 Mathamatics I,MATH 301601 Partial Differential Equations,23565 Mathematics for Economics and Business,Math 506 Stochastic Analysis for Finance,MTH 4430 – Mathematics of Inferential Statistics,MATH 126 A Calculus With Analytic Geometry III,MA-451 Differential Equations,STAT2602 PROBABILITY AND STATISTICS II,MATH 110, Linear Algebra,MAT 067 Modern Linear Algebra,Math 115A Fall2020 linear algebra,MATH2102 Linear algebra II,MATH 305 Advanced Linear Algebra,MATH5003 Linear Algebra and Numerical Analysis,MA1503 Linear Algebra with Applications,MAT 223 Linear Algebra,MAST10007 Linear Algebra,MATA22 Linear algebra Midterm I,Math 211 matrix algebra,Math 312 complex analysis,MAT 2324 Ordinary Differential Equations and Laplace Transform,AMA 2111 Mathamatics I,MATH2012 Fundamental Concepts of Mathematics,Math 135 Algebra for Hons Mathematics,Algebra MATH-UA.0343,MA2014 Algebra I,MATH 150B (Modern Algebra),Math 3110/6110,MATH 2001 Advanced Calculus and Linear Algebra II,MA3304 Method of Applied Mathematics,Math 596 Complex Analysis,Math 555 Intro to Complex Variables,Math5825 Measure Integration and Probability,SEHH1069 Calculus and Linear Algebra,EC1109 Mathematics for Economics,AMA3721 Probability and Distributions for Risk Management,CS2402 Introduction to Computational Probability Modeling,ECE302 Probabilistic Methods in Electrical and Computer Engineering,Math 2501, Spring 2021 Elementary Probability and Statistics,MATH-UA.0233-001 Theory of Probability,Probability & Statistics in Engineering (CIVL2530),Numerical Methods in Engineering (ENGR20005),Maths2107 I II,MATH-UA.0252 Numerical Analysis,Math 97113 Random process,Math 330 scientific computing,MA1200 Calculus and Basic Linear Algebra I,Math 2069 Vector calculus & Complex analysis,Math 54 Linear Algebra and Differertial Equations,STAT2602 PROBABILITY AND STATISTICS II ……
数学科目真滴实在是太多了,我就不一一列举了,现在发现之前接过的科目压根就数不完了!hhhh
后面类别也只写一小部分吧,实在是太多了。。。
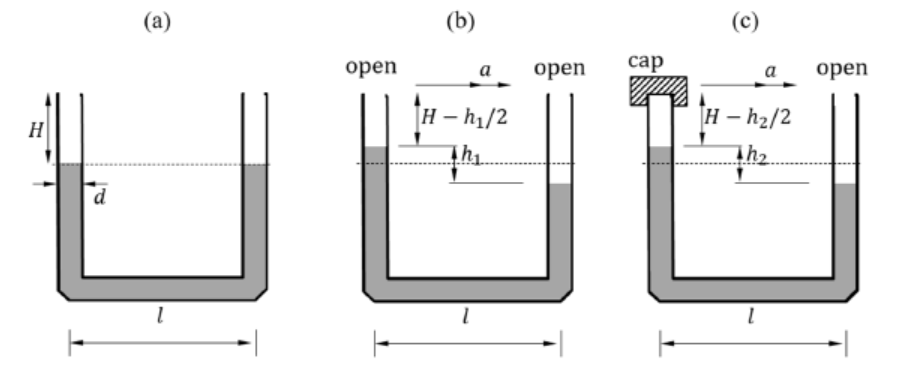
物理类:Physics Bowl,Australian Science Olympiads – Physics(ASOP),PX2620 Quantum Mechanics and its Applications,PHYS1121 Physics 1A,PHYS 100 Introductory Physics,PHYS2130 PHYSICS A,Physics 1112,Physics 1114,MATH0025 Mathematics For General Relativity,SEHH1049 Physics I,PHAS0038 – Electromagnetic Theory,PHAS0041-Solid State Physics,PHAS0042 Quantum Mechanics,PHY132 Introduction to Physics II,PHYS 102 D100 PHYSICS FOR THE LIFE SCIENCES II,PHY1001 Mechanics,PX275 Mathematical Methods,PX265-7.5 Thermal Physics II,PHYS96010 Compuational Physics,PHYS 2040 – RELATIVITY AND MODERN PHYSICS,PHYS 301605 Partial Differential Equations EXAM 1,PX145 PHYSICS FOUNDATIONS,PX1200 Electricity and Magnetism,PHAS0010 Classical Mechanics,Engineering Electromagnetics ELEC ENG 3103,PHY2049 Calculus-based Physics II,68201 Physics in Action,Physics 115a,Pyhsics 9B,Physics 141A,Physics 1201,Physics 1221,Physics 221,Physics 521,Physics 5C,PHYS 304,Physics 10004,Physics 8B,,Physics 1C,Physics 9A,Physics 1A……
化学类:The Avogadro Exam,Canadian Chemistry Contest,CHEM 40A – Organic Chemistry I,CHEM 40B Organic Chemistry II,CHEM 261 – Organic Chemistry I,CHEM0008 – Basic Organic Chemistry,CHEM0016 – Organic Chemistry,CHEM50007 Control and Selectivity in Molecular Synthesis,CHEM1011 Fundamentals of Chemistry 1A,CHEM CHEM-102 General Chemistry IB ,CHEM 1030General Chemistry II,CHEM2541 Introductory physical chemistry,CHEM0009 Basic Physical Chemistry,CHEM 123 – Thermodynamics, Kinetics and Organic Chemistry,FC304 Chemistry,HPHS4002 College Chemistry for Medical and Health Products Sciences,CHEM20020 Structure and Properties,CHEM20018 Reactions and Synthesis,CHEM 205 Final physical chemistry,CHEM025 Advanced Topic In Organic Chemistry,CH-237 FURTHER PHYSICAL CHEMISTRY,CH-238 Further Organic ChemistryCH-238 Further Organic Chemistry,CHEM 1022,CHEM 4420,Chemistry 1B,CHEM 233 – Organic Chemistry for the Biological Sciences……
金融经济类:ECON90033 QUANTITATIVE ANALYSIS OF FINANCE I,Fall 2020 Econ 140A,23568 Intermediate Macroeconomics,ECON2210 C&D Intermediate Microeconomics,ECON1210 Introductory Microeconomics,EC5040 Econometrics,ECON0019 – Quantitative Economics and Econometrics,MGEC81 Economic Development,ECON 120A Econometrics A,MA3503 Stochastic Processes of Finance and Insurance,BU.232.620.F1 – Linear Econometrics for Finance,ECON 162 001 The Chinese Economy,ENVECON 118 Introductory Applied Econometrics,23571 Introductory Econometrics,FOUNDATION ECONOMICS Macroeconomics,EC 611 The Macroeconomics of Financial Markets,BUS104 Economics,Intermediate Microeconomics 23567,Econ 201,UN3211 Intermediate Microeconomics,ECO 2013,FIN0008 Managing Business Finance,FIN5004 Financial Trading,MFIN 6210 Empirical Studies in Finance,ASB3208 Financial Statement Analysis,EFIMM0110 FINANCIAL MARKETS AND INVESTMENTS,ACFI312 Business Strategy,BHMH2113 Financial Management,HPMS4008-HL01 International Trade,CB2300 Management,FINC11-101 FUNDAMENTALS OF FINANCE,N1591 Valuation of Companies and Cash Flow Generating Assets,HPMS4005 Fundamentals of Finance,valuation of companie,BUS 312 – Introduction to Finance,ACCT5930 Financial Accounting,ACFI301 Advanced Auditing,ADVANCED MANAGEMENT ACCOUNTING N1551……
计算机:COMP 2011 C++,CS2310 202021 ,SEHH2042 Computer Programming,CB2240 – Introduction to Business Programming in Python,COMP1117B Computer Programming,DSC 20 – Prgrmng DataStruc for Data Sci,COP 3530 – DATA STRUCTURES AND ALGORITHMS,DSC 20 – Prgrmng DataStruc for Data Sci ,CSCA48,COP 3502,CS 2360 Java Programming,Introduction to Computing II (ITI 1121)……
电气工程:ELEC2133 Analogue Electronics,Systems Modelling and Analysis (MCEN30020),System Control Design,EE 241A Stochastic Processes,ELEC 2400 ELECTRONIC CIRCUITS,ELEC3200 System Modeling, Analysis and Control,ELEC2134 Electrical and Telecommunications Engineering,ECE 1240 Intro to circuit design,ELEC0021-Programming and Control Systems,ECE 2020 – Introduction to Analog Systems and Circuits,ENG3012 Engineering,ELEC3100 Signal Processing and Communications,Introduction to electrical engineeringElectrical machines,PGEE10018 DISCRETE-TIME SIGNAL ANALYSIS,Communication Systems ECE 151,ECE 103 Signals and Systems,CSE100 Logic Design,Control (Elec Eng 31017082),ETM 3061 ‐ Applied Thermodynamics I,TELE4653 Digital Modulation & Coding,ITI1100–Digital Systems I,ECSE-2410 Signals ans System,ECSE-2111 Signals ans System,EE 520 Random Processes,ECE322,CIVL2120 Mechanics of Materials,MECH3610 Advanced Thermofluids,MCEN30018 Fluid Mechanics and Thermodynamics,ELEC ENG2104 Digital Signal Processing……
再次感谢各位家人们的信任与支持!有任何需求都可以及时联系我们🥰
代写之家,您值得信赖的代写代考专家😝
代写之家为海外留学生提供全方面的线上辅导,包括但不限于:exam代考、留学生考试、代考, 作业代写,留学生作业代写, 网课代上、网课代考,致力于提升Exam/Quiz分数并向更高GPA冲刺。同时提供考试辅助等在线解题服务